选择困难者的福音？层次分析法

| | |
2.2k | 8

摘要

日常生活中，我们面临很多的选择，选择自己最工作offer，选择买哪个牌子的手机，选择哪个地方旅行等等。这些选择难以定量的衡量，有很多不确定性。内心小纠结，我选择了这个，万一那个好呢，怎么办？请看层次分析法。

层次分析法(Analytic Hierarchy Process，简称 AHP)是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。它是美国运筹学家 T. L. Saaty 教授于上世纪 70 年代初期提出的一种简便、灵活而又实用的多准则决策方法。

运用层次分析法建模，大体上可按下面四个步骤进行

  • 建立递阶层次结构模型
  • 构造出各层次中的所有判断矩阵
  • 层次单排序及一致性检验
  • 层次总排序及一致性检验。（一般不用）

让我们从offer大佬的例子开始吧！

举个栗子，今年有位大学生，有三个offer，C1 C2 C3。

第一步，建立层次模型。

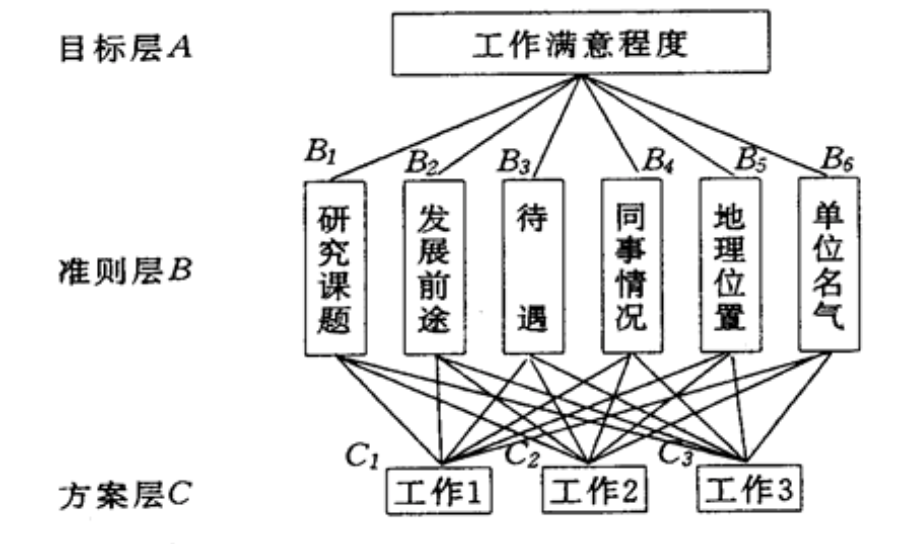
  • 目标层A：找工作的目标，自己满意程度。
    • 这个程度怎么计算呢？比如工作1。
  • 准则层B：研究课题、发展前途、待遇、同事情况、地理位置、单位名气等等。
    • 尽量列全一点，不需要排列重要顺序。
    • 小于等于9个，后面要两两拍脑袋给出相对的重要层度，给多了不得把脑袋拍疼了。
    • 也可以有子准则层，比如待遇中的放假、工作环境等等，列出也小于9个。
  • 方案层C：就是我们的offer
image-20200406145535585

构造 A B 之间判断矩阵

准则层B与目标A之间的关系。为了求出准则层中(B1-6) 对目标的重要层度的排序。比如对于该生工作满意度第一重要是待遇，然后是地点，其实该生自己也很模糊。就是固定A，然后求B中准则，对A重要性的排序。

我们怎么对B中的准则们的重要排序呢？

直接给每一个准则，0-1的评分，然后排序。经常会想，给完分之后，这个不合理呀要不我再给哪个准则加加分。所以这样的方法常常会因考虑不周全、顾此失彼而使决策者提出与他实际认为的重要性程度不相一致的数据。

我们可以将这个过程细化，我就比较两个准则对于目标的重要性，然后通过下面的矩阵方法，求出优先顺序。

还能通过一个一致性检验，来检验在你评分的过程中，有没有自相矛盾的地方，当然这种方法允许一些自相矛盾。反正评分的时候尊从内心拍脑袋就对了。

所以我们拿出一个B1 与 B2 对于目标的重要，想一想然后给出B2/B1，填入下面的表格中的(2,1)的位置。

整个矩阵i,j 与j，i 是取倒数的关系，所以只要做一半。

在找工作的目标下，准则i与j相对的重要性表示，B2/B1 的值。采用9个标度。而相比不重要刻度取倒数就可以了

准则i比j的比较123456789
相同重要比较重要明显重要强烈重要极端重要

最后的两两相对重要表格

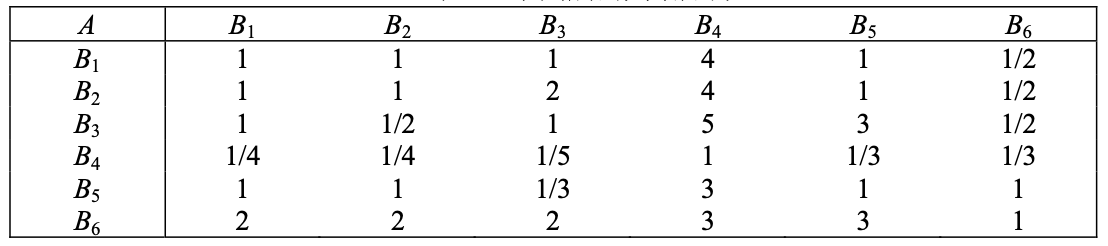
image-20200406145640316

对角线对称的两个数互为倒数，即 $$a_{ji}=\frac{1}{a_{ij}}$$ B1/B2 不就是和 B2/B1互为倒数嘛

从心理学观点来看，分级太多会超越人们的判断能力，既增加了作判断的难度， 又容易因此而提供虚假数据。Saaty 等人还用实验方法比较了在各种不同标度下人们判断结果的正确性，实验结果也表明，采用 1~9 标度最为合适。

判断矩阵的一致性指标步骤：

  • 1）计算一致性指标 CI 。$$CI=\frac{ \lambda_{max}-n}{n-1}$$
  • 2）查表，平均随机一致性指标 RI。
n123456789
RI000.580.901.121.241.321.411.45

RI 的值是这样得到的，用随机方法构造500个样本矩阵:随机地从1~9及其倒数中抽取数字构造正互反矩阵，求得最大特征根的平均值 $$\bar \lambda_{max}$$ 并定义$$RI=\frac{\bar \lambda_{max}-n}{n-1}$$

  • 3）计算一致性比例CR。 $$CR=\frac{CI}{RI}$$，当$$CR<0.10$$ 时，认为判断矩阵的一致性是可以接受的，否则应对判断矩阵作适当修正。

如果一个矩阵满足上面的条件，那么它最大特征值对应的特征向量就可以认为是每个维度的重要性权重。

构造 B C 之间判断矩阵

相同的方法，在同一B准则下，考虑不同工作的优先顺序。求工作排序的方法，和上面一样。

image-20200406162644137

python代码[1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
import numpy as np
import pandas as pd
import warnings


class AHP:
    def __init__(self, criteria, b):
        self.RI = (0, 0, 0.58, 0.9, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49)
        self.criteria = criteria
        self.b = b
        self.num_criteria = criteria.shape[0]
        self.num_project = b[0].shape[0]

    def cal_weights(self, input_matrix):
        input_matrix = np.array(input_matrix)
        n, n1 = input_matrix.shape
        assert n == n1, '不是一个方阵'
        for i in range(n):
            for j in range(n):
                if np.abs(input_matrix[i, j] * input_matrix[j, i] - 1) > 1e-7:
                    raise ValueError('不是反互对称矩阵')

        eigenvalues, eigenvectors = np.linalg.eig(input_matrix)

        max_idx = np.argmax(eigenvalues)
        max_eigen = eigenvalues[max_idx].real
        eigen = eigenvectors[:, max_idx].real
        eigen = eigen / eigen.sum()

        if n > 9:
            CR = None
            warnings.warn('无法判断一致性')
        else:
            CI = (max_eigen - n) / (n - 1)
            CR = CI / self.RI[n]
        return max_eigen, CR, eigen

    def run(self):
        max_eigen, CR, criteria_eigen = self.cal_weights(self.criteria)
        print('准则层：最大特征值{:<5f},CR={:<5f},检验{}通过'.format(max_eigen, CR, '' if CR < 0.1 else '不'))
        print('准则层权重={}\n'.format(criteria_eigen))

        max_eigen_list, CR_list, eigen_list = [], [], []
        for i in self.b:
            max_eigen, CR, eigen = self.cal_weights(i)
            max_eigen_list.append(max_eigen)
            CR_list.append(CR)
            eigen_list.append(eigen)

        pd_print = pd.DataFrame(eigen_list,
                                index=['准则' + str(i) for i in range(self.num_criteria)],
                                columns=['方案' + str(i) for i in range(self.num_project)],
                                )
        pd_print.loc[:, '最大特征值'] = max_eigen_list
        pd_print.loc[:, 'CR'] = CR_list
        pd_print.loc[:, '一致性检验'] = pd_print.loc[:, 'CR'] < 0.1
        print('方案层')
        print(pd_print)

        # 目标层
        obj = np.dot(criteria_eigen.reshape(1, -1), np.array(eigen_list))
        print('\n目标层', obj)
        print('最优选择是方案{}'.format(np.argmax(obj)))
        return obj


if __name__ == '__main__':
    # 准则重要性矩阵
    criteria = np.array([[1, 2, 7, 5, 5],
                         [1 / 2, 1, 4, 3, 3],
                         [1 / 7, 1 / 4, 1, 1 / 2, 1 / 3],
                         [1 / 5, 1 / 3, 2, 1, 1],
                         [1 / 5, 1 / 3, 3, 1, 1]])

    # 对每个准则，方案优劣排序
    b1 = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])
    b2 = np.array([[1, 2, 5], [1 / 2, 1, 2], [1 / 5, 1 / 2, 1]])
    b3 = np.array([[1, 1, 3], [1, 1, 3], [1 / 3, 1 / 3, 1]])
    b4 = np.array([[1, 3, 4], [1 / 3, 1, 1], [1 / 4, 1, 1]])
    b5 = np.array([[1, 4, 1 / 2], [1 / 4, 1, 1 / 4], [2, 4, 1]])

    b = [b1, b2, b3, b4, b5]
    a = AHP(criteria, b).run()

层次分析法与控制变量法

我们的任务是选择工作，最后使得我们满意，直接选择我们当然一头雾水。所以我们设立一些准则，然后对这些准则对于目标的重要性排序。

这又有点像概率图模型，只是赋权的方法，是相互比较的方法。

选择困难者的福音？

层次分析法对人们的思维过程进行了加工整理，提出了一套系统分析问题的方法，为科学管理和决策提供了较有说服力的依据。

在应用层次分析法研究问题时，遇到的主要困难有两个:
(1) 如何根据实际情况抽象出较为贴切的层次结构;
(2) 如何将某些定性的量作比较接近实际定量化处理。

层次分析法的其局限性[2]：
(1) 它在很大程度上依赖于人们的经验，主观因素的影响很大，它至多只能排除思维过程中的严重非一致性，却无法排除决策者个人可能存在的严重片面性。
(2) 比较、 判断过程较为粗糙，不能用于精度要求较高的决策问题。

所以，AHP 至多只能算是一种半定量(或定性与定量结合)的方法。 本文仅供参考，不负法律责任，哈哈。

参考

  1. 幼鹰me 知乎 层次分析法原理与Python实现 ↩︎

  2. 司守奎《数学建模算法与程序》第八章 层次分析法 P167 ↩︎

0%